|
Content
This page contains a brief discussion of the background for, the functionalities available in,
and the organization of our serial coloring software package ColPack. For a detailed discussion
of the algorithms on which the package relies, consult the Papers page.
Sparse
derivative computation and coloring
Four-step procedure
The computation of an m-by-n
sparse derivative matrix A using automatic
differentiation (AD) can be made efficient by using the following
four-step procedure.
- Determine the sparsity structure of A.
- Using a
specialized vertex coloring
on an appropriate graph representation of the matrix A, obtain an n-by-p seed
matrix S that defines a partitioning of the columns of A into p groups with p as small as possible.
- Compute the compressed matrix B = AS using AD.
- Recover the numerical
values of the entries of A from B.
The set of criteria used to define the seed matrix S
in the second step, the partitioning problem on the matrix A,
depends on three mutually orthogonal factors:
- Whether the
derivative matrix being computed is a Jacobian (nonsymmetric) or a Hessian (symmetric),
- Whether the
numerical values of the entries of the original matrix A are obtained from the compressed representation B directly
(without any further arithmetic) or indirectly (for example, by solving for unknowns via
successive substitution), and
- Whether the
matrix partitioning is unidirectional
(involving only columns or only rows) or bidirectional (involving both columns and rows). The
four-step procedure above is described assuming a column-wise
unidirectional partitioning. In a row-wise unidirectional
partitioning (which is a better approach for Jacobian matrices
with a few dense rows), the compressed matrix would correspond to
the seed-matrix-Jacobian product STA.
Similarly, in a bidirectional partitioning (which might be the
best approach for Jacobian matrices with both a few dense rows and
a few dense columns), the Jacobian entries are recovered from two
compressed matrices S1TA
and AS2.
Coloring models
Table 1 below provides a summary of the most
accurate coloring models for the various computational scenarios. In
each case, the structure of a Jacobian matrix A is represented
by the bipartite graph Gb(A) = (V1,
V2, E), where the vertex sets V1 and
V2 represent the rows and columns of A,
respectively, and each nonzero matrix entry Aij is
represented by the edge (ri , cj)
in E. Analogously, the structure of a Hessian matrix A
is represented by the adjacency
graph G(A) = (V, E), where the vertex set V
represents the columns (or, by symmetry, the rows) of A
and each off-diagonal nonzero matrix entry Aij
(and its symmetric counterpart Aji)
is represented by the single edge (ci, cj)
in E.
|
|
1d partition
|
2d partition
|
|
|
Jacobian
|
Partial
distance-2 coloring
|
Star
bicoloring
|
Direct
|
|
Hessian
|
Star coloring
|
NA
|
Direct
|
|
Jacobian
|
NA
|
Acyclic
bicoloring
|
Substitution
|
|
Hessian
|
Acyclic
coloring
|
NA
|
Substitution
|
Table 1: Overview of
coloring models in derivative computation. NA
stands for not applicable.
In a graph G = (V, E), two distinct
vertices are distance-k neighbors if a shortest
path connecting them consists of at most k edges. A distance-k coloring of the graph is an assignment of positive
integers (called colors) to the vertices such that every two distance-k
neighboring vertices get different colors. A star coloring is a distance-1 coloring where, in addition,
every path on four vertices uses at least three colors. An acyclic coloring is a distance-1
coloring in which every cycle uses at least three colors. The names
star and acyclic coloring are due to the structures of two-colored induced subgraphs: a
collection of stars in the case of star coloring and a collection of
trees in the case of acyclic coloring.
In a bipartite graph Gb = (V1,
V2, E), a partial
distance-2 coloring on the vertex set Vi, i = 1,2,
is an assignment of colors to the vertices in Vi such
that any two vertices connected by a path of length exactly two edges
receive different colors. Star
and acyclic bicoloring in a bipartite graph are defined in a manner
analogous to star and acyclic coloring in a general graph, but with the
additional stipulation that the set of colors assigned to row vertices
(V1) is disjoint from the set of colors used
for column vertices (V2).
ColPack : functionalities
ColPack is a package comprising of implementations of
algorithms for the specialized vertex coloring problems discussed in
the previous section as well as algorithms for a variety of related
supporting tasks in derivative computation.
Coloring capabilities
Table 2 below gives a quick summary of all the coloring
problems (on general and bipartite graphs) supported by ColPack.
|
General
Graph G = (V, E)
|
Bipartite Graph Gb = (V1, V2, E):
One-sided
Coloring
|
Bipartite Graph Gb = (V1, V2, E):
Bicoloring
|
|
·
Distance-1 coloring
O(|V|∙d1) = O(|E|)
|
·
Partial
distance-2 coloring on V2
O(|V2|· d(V2)
· Δ(V1)) = O (|E|·Δ(V1))
|
·
Star
bicoloring†
O((|V1|+ |V2|)∙d2))
|
|
·
Distance-2
coloring
O(|V|∙d2)
|
·
Partial
distance-2 coloring on V1
O(|V1|· d(V1)
· Δ(V2)) = O(|E|·Δ(V2))
|
|
|
·
Star coloring†
O(|V|∙d2)
|
|
|
|
·
Acyclic
coloring
O(|V|∙d2∙α)
|
|
|
|
·
Restricted
star coloring
O(|V|∙d2)
|
|
|
|
·
Triangular
coloring†
O(|V|∙d2)
|
|
|
Table
2: List of coloring problems for which implementations of algorithms
are available in ColPack. Problems with the superscript †
have more than one algorithm implemented in ColPack; the complexity
listed in each case is that of the fastest algorithm.
All of the coloring problems listed in Table 2 are
NP-hard. Their corresponding algorithms in ColPack are greedy heuristics in the sense
that the algorithms progressively extend a partial coloring by
processing one vertex at a time, in some order, in each step assigning
a vertex the smallest allowable color. Listed beneath each coloring
problem in Table 2 is the complexity of the corresponding algorithm in
ColPack. In the cases where ColPack has multiple algorithms for a
problem (these are designated by the superscript †), the
complexity expression corresponds to that of the fastest algorithm. In
the complexity expressions,
- dk denotes the average degree-k, the number of distinct paths of length at most k edges leaving a vertex. Thus d1(v) corresponds to the usual degree
of the vertex v, the number of edges incident on v, and d2(v)
corresponds to the sum of the degree-1 values of the vertices
adjacent to v.
- α denotes the inverse of Ackermann’s
function.
- d(Vi) and Δ(Vi)
denote the average and maximum, respectively, vertex degree-1 in
the set Vi, i=1,2,
of the bipartite graph Gb = (V1,
V2 , E).
Ordering techniques
The order in which vertices are processed in a
greedy coloring algorithm determines the number of colors used by the
algorithm. ColPack has implementations of various effective ordering
techniques for each of the supported coloring problems. These are
summarized in Table 3 below.
|
General
Graph
|
Bipartite
Graph: One-sided Coloring
|
Bipartite
Graph: Bicoloring
|
|
·
Natural
|
·
Column Natural
|
·
Natural
|
|
·
Largest First
|
·
Column Largest
First
|
·
Largest First
|
|
·
Smallest Last
|
·
Column
Smallest Last
|
·
Smallest Last
|
|
·
Incidence
Degree
|
·
Column
Incidence Degree
|
·
Incidence
Degree
|
|
·
Dynamic
Largest First
|
·
Row Natural
|
·
Dynamic
Largest First
|
|
·
Distance-2
Largest First
|
·
Row Largest
First
|
·
Selective
Largest First
|
|
·
Distance-2 Smallest
Last
|
·
Row Smallest
Last
|
·
Selective
Smallest Last
|
|
·
Distance-2
Incidence Degree
|
·
Row Incidence
Degree
|
·
Selective
Incidence Degree
|
|
·
Distance-2
Dynamic Largest First
|
|
|
Recovery routines
Besides coloring and ordering capabilities, ColPack
also has routines for recovering the numerical values of the entries of
a derivative matrix from a compressed representation. In particular the
following reconstruction routines are currently available:
- Recovery
routines for direct (via star coloring ) and substitution-based
(via acyclic coloring) Hessian computation
- Recovery
routines for unidirectional, direct Jacobian computation (via
column-wise or row-wise distance-2 coloring)
- Recovery
routines for bidirectional, direct Jacobian computation via star
bicoloring
Graph construction routines
Finally, as a supporting functionality, ColPack has
routines for constructing bipartite graphs (for Jacobians) and
adjacency graphs (for Hessians) from files specifying matrix sparsity
structures in various formats, including Matrix Market, Harwell-Boeing
and MeTis.
ColPack : organization
ColPack is written in an object-oriented fashion in
C++ heavily using the Standard Template Library (STL).
It is designed to be simple, modular, extensible and efficient.
Figure 1 below gives an overview
of the structure of the major classes of ColPack.
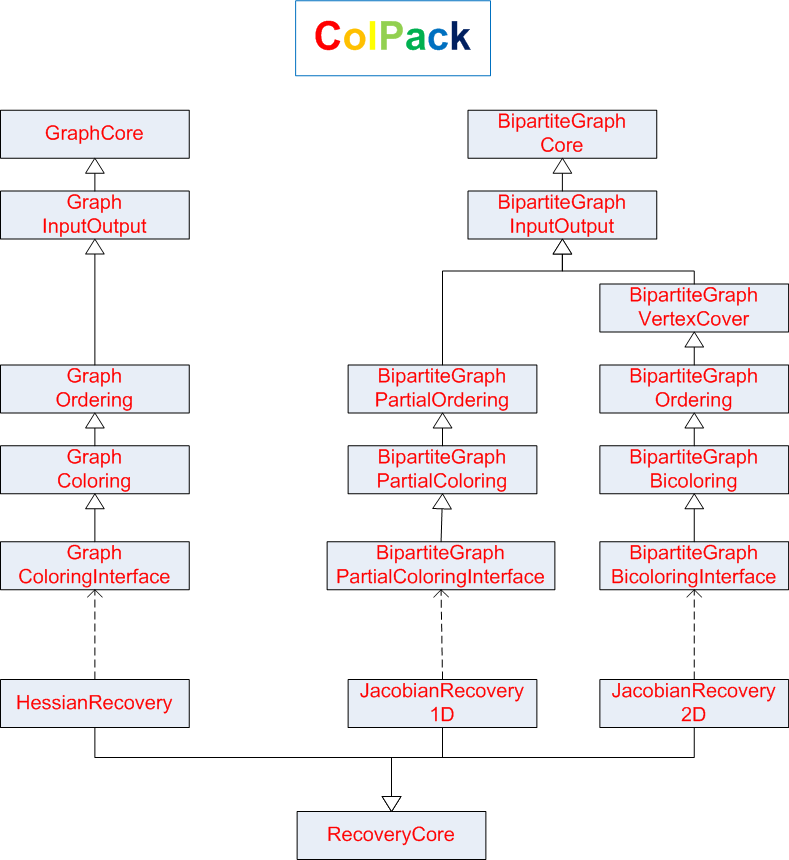
Figure 1: Overview of the
structure of the major classes in ColPack. A solid arrow indicates an
inheritance-relationship, and a broken arrow indicates a
uses-relationship.
ColPack functions that a user needs to call
directly are made available via the appropriate Interface classes.
Sample Codes
The following sample codes illustrate how ColPack
functions are called in the context of sparse derivative computation
via the Four-step Procedure. In each sample code, the de-compressed sparse derivative matrix is
returned in the Coordinate Format (zero-based indexing).
Recovery routines that return the de-compressed matrix in
Direct Sparse Solver and ADOL-C Formats are also available in ColPack.
Column-wise Jacobian Computation (via partial
distance-2 coloring)
Row-wise Jacobian Computation (via partial distance-2
coloring)
Direct Hessian Computation (via star coloring)
Indirect Hessian Computation (via acyclic coloring)
Bidirectional, direct Jacobian Computation (via star
bicoloring)
Download
Here is the source code of ColPack. It is being distributed under the GNU Lesser General Public
License.
ColPack
And here are a few test graphs for experiments.
Graph
Collection in MeTis format
Graph
Collection in Matrix Market format
Complete Doxygen documentation of ColPack
|